“scratch還可以這樣啊！”一位媽媽在看到自己的孩子用編程解決了一個古老的數(shù)學(xué)問題百錢買百雞，驚喜地發(fā)出這樣的感嘆。

公雞5錢一只，母雞3錢一只，小雞1錢三只，共有100錢數(shù)，要求如何用100錢買100只雞，且要求公雞、母雞、小雞都有。問要買公雞多少只？母雞多少只？小雞多少只？

從現(xiàn)代數(shù)學(xué)觀點來看，實際上是一個求不定方程整數(shù)解的問題。解法如下：

設(shè)公雞、母雞、小雞分別為x、y、z 只，由題意得：有兩個方程，三個未知量，稱為不定方程組，則有多種解。

①……x+y+z =100

②……5x+3y+(1/3)z =100

下面再看看x，y，z的取值范圍。

由于只有100錢，由5x<100?=>?0<="" p="">

那如何用scratch來解決這一問題呢？新建三個變量“公雞的數(shù)量”、“母雞的數(shù)量”、“小雞的數(shù)量”，作為小學(xué)生可能還不能夠深刻理解用變量來表示算數(shù)表達式，如果類比數(shù)學(xué)應(yīng)用題中的設(shè)未知數(shù)“x”、“y”、“z”，這便容易理解多了，這道題便是這樣，可以得到兩個關(guān)于變量的算數(shù)表達式。

百錢買百雞最適宜學(xué)習(xí)窮舉法（枚舉法），所謂窮舉法，顧名思義窮盡每一種可能性，通常在找不到解決問題的規(guī)律時對可能是解的眾多候選解按照某一順序進行逐一枚舉和檢驗，并從中找出那些符合要求的候選解作為問題的解。考慮到算法的時間復(fù)雜度與空間復(fù)雜度還可以不斷優(yōu)化，方法并不唯一。

scratch擁有計時器的功能，可以更加直觀的將程序執(zhí)行所需時間顯示出來。

方法一：x的取值范圍為1~20, y的取值范圍為1~33，z的取值范圍為3~99（以3的數(shù)量增加），利用三層循環(huán)嵌套遍歷x、y、z的所有可能的組合。程序執(zhí)行完成所花費的時間約為4秒，當(dāng)然也可以簡化此程序。

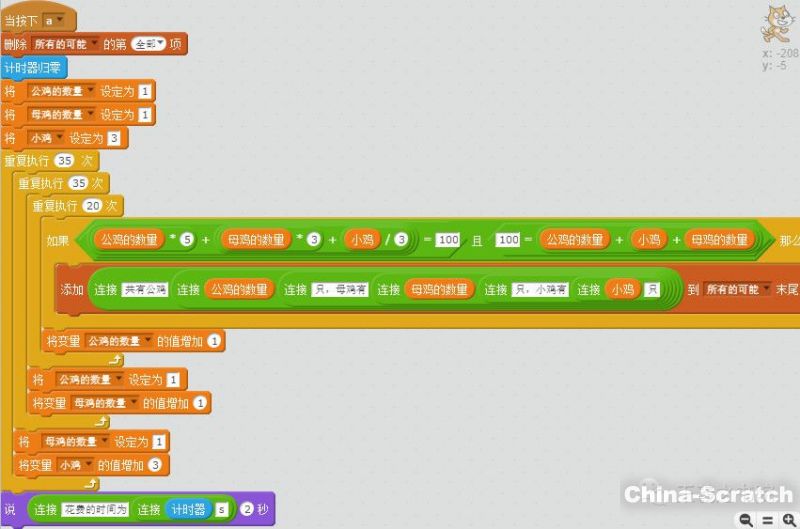
方法二：公雞的數(shù)量為x,母雞的數(shù)量為y,小雞的數(shù)量為z,從1開始窮舉小雞與母雞的數(shù)量，則公雞的數(shù)量為x=100-y-z，只需要兩層循環(huán)嵌套便可實現(xiàn)。程序執(zhí)行完成所花費的時間約為0.5秒。

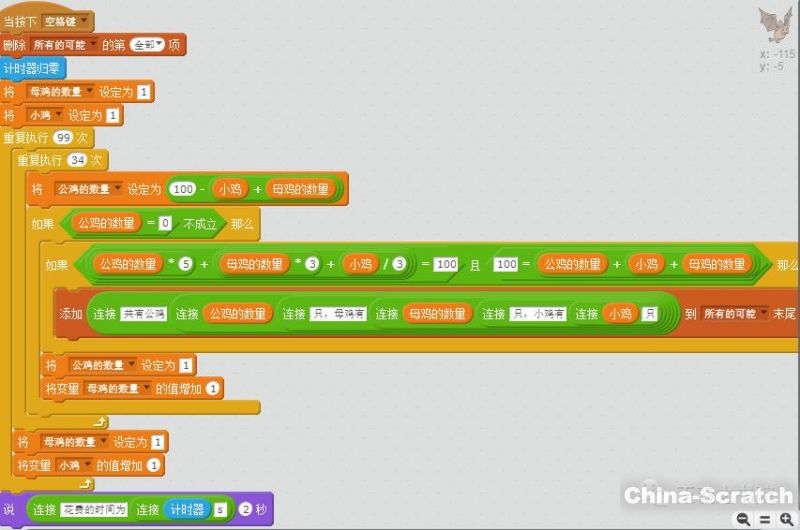
方法三：一層循環(huán)的實現(xiàn)方法需要推算一下這個不定方程。

? ? x+y+z=100 ? ? ? ? ?①

? ? 5x+3y+z/3=100 ? ?②

?令②x3-① 可得

? ? 7x+4y=100

=>? ? ? ? ? ? ? ??y=25-(7/4)x ??? ? ? ?③

同理可推得? ?

?=>??? ? ? ? ? ? ?z=75+(3/4)x??? ? ? ?④

程序執(zhí)行完成所花費的時間約為0.01秒。

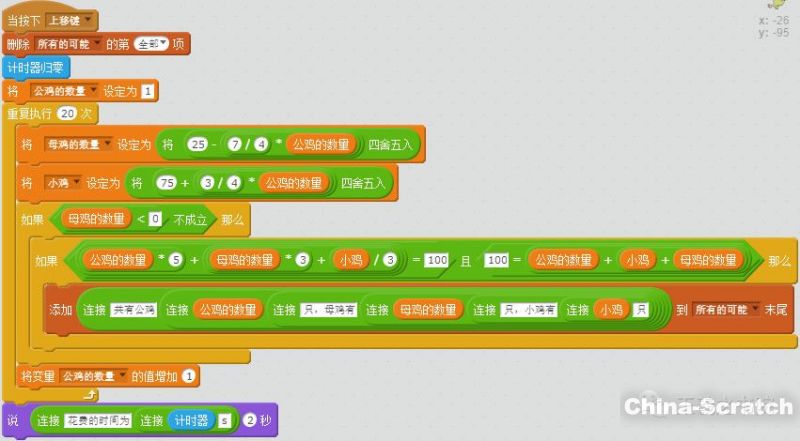
學(xué)生通常會帶給老師很多啟發(fā)，這比老師帶給學(xué)生的更具沖擊感。解決這一問題，可能是根深蒂固的固有思維，我們往往窮舉雞的數(shù)量，但是，一次上課，一位同學(xué)設(shè)的變量為每種雞所花費的錢數(shù)，于是豁然開朗。

方法四：利用三層循環(huán)嵌套窮舉錢數(shù)，程序執(zhí)行完成所花費的時間約為9.3秒。當(dāng)然還可以繼續(xù)改進該程序，用兩層循環(huán)或者一層循環(huán)均可。

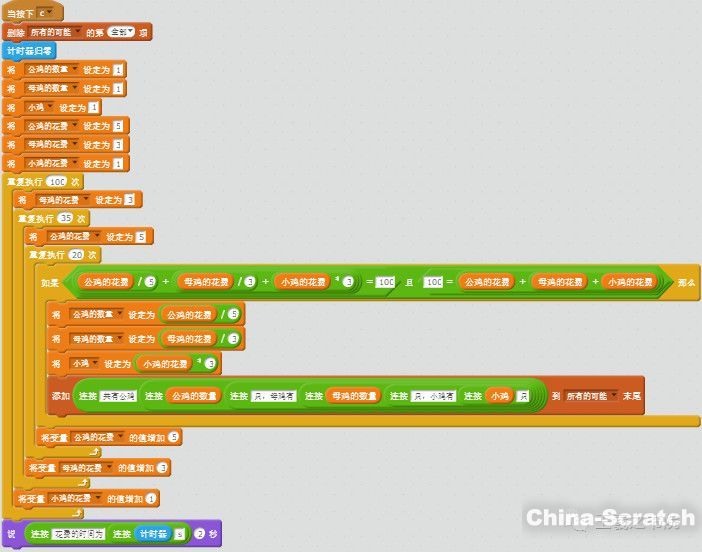
考慮到每種雞都要有，則共有3組數(shù)成立：

4只公雞18只母雞78只小雞

8只公雞11只母雞81只小雞

12只公雞4只母雞84只小雞

聲明：本文章由網(wǎng)友投稿作為教育分享用途，如有侵權(quán)原作者可通過郵件及時和我們聯(lián)系刪除