哈嘍大家好，歡迎再次回到我們的課堂，這節(jié)課咖姐帶領(lǐng)大家學(xué)習(xí)如何用scratch來求取兩個數(shù)的最大公約數(shù)。

在此做項目之前，我們先來了解一下定義：

最大公約數(shù)：也稱最大公因數(shù)、最大公因子，指兩個或多個整數(shù)共有約數(shù)中最大的一個。比如4和6的最大公約數(shù)就是2，而4和8的最大公約數(shù)就是4。

求最大公約數(shù)有多種方法，常見的有質(zhì)因數(shù)分解法、短除法、輾轉(zhuǎn)相除法、更相減損法。

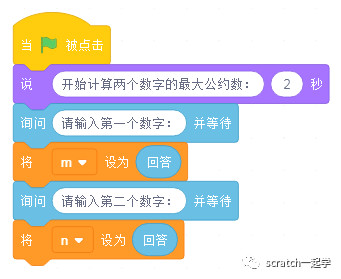
想要實現(xiàn)想要的功能，首先必須有兩個數(shù)字，這兩個數(shù)字是未知的，我們需要手動輸入，所以可通過“詢問...并等待”積木塊來實現(xiàn)，同樣的，我們也需要兩個變量來接受這兩個數(shù)字，具體的代碼如下：?

那么接下來，我們需要進(jìn)行考慮用哪種方法來實現(xiàn)求取最大公約數(shù)的功能，我們已經(jīng)知道有很多種方法，今天我們用更相減損法來實現(xiàn)最大公約數(shù)的求取。

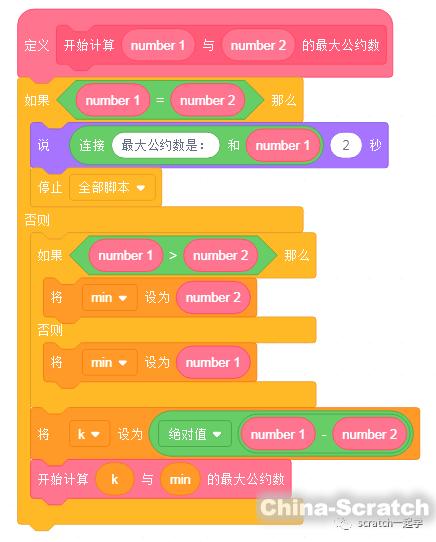
　更相減損法：也叫更相減損術(shù)，是出自《九章算術(shù)》的一種求最大公約數(shù)的算法，就是對于給定的兩個數(shù)，用較大的數(shù)減去較小的數(shù)，然后將差和較小的數(shù)構(gòu)成新的一對數(shù)，再用較大的數(shù)減去較小的數(shù)，反復(fù)執(zhí)行此步驟直到差數(shù)和較小的數(shù)相等，此時相等的兩數(shù)便為原來兩個數(shù)的最大公約數(shù)。

從上面的定義我們也知道，要反復(fù)比較差值和最小數(shù)的大小，那么這里我們就要用到一個新的計算方法----遞歸。

遞歸：就是在運行的過程中調(diào)用自己。

構(gòu)成遞歸需具備的條件：

1. 子問題須與原始問題為同樣的事，且更為簡單；

2. 不能無限制地調(diào)用本身，須有個出口，化簡為非遞歸狀況處理。

同樣的，使用遞歸時我們需要一個函數(shù)。一個較大的程序一般應(yīng)分為若干個程序塊，每一個模塊用來實現(xiàn)一個特定的功能，而這每個每個模塊都可以看成一個子函數(shù)，這個大的程序可以看成一個主函數(shù)。具體的函數(shù)形式在我們scratch中是以“自制積木”來實現(xiàn)的。

按照我們更相減損法的定義，可以做出具體的代碼如下：

同樣的，我們需要在程序開始時調(diào)用這個函數(shù)，具體代碼如下：

求取最大公約數(shù)的程序以及完成，趕緊試一下吧。

我們知道有多種求取公約數(shù)的方法，那么你能夠運用別的方法實現(xiàn)同樣的功能嗎？試一試吧

聲明：本文章由網(wǎng)友投稿作為教育分享用途，如有侵權(quán)原作者可通過郵件及時和我們聯(lián)系刪除