資訊內容
為什么編程啟蒙要學 Scratch?


要回答這個問題,我們先來看看Scratch是什么?
歐美在打造孩子的未來創新能力上有很多創新的項目。比如樂高教育,專注于用物理世界的結構搭建;樂高WeDo,專注于機器人編程;Tickle,專注于智能硬件;Scratch,專注于提供適用于兒童的編程語言和工具。其中最為突出的當數 Scratch。?

Scratch 編程語言是由麻省理工大學 MIT 和 Google 主導開發的針對 5-12 歲兒童的可視化編程語言。只需要使用鼠標,學生就可以編寫自己的故事書,動畫片或者小游戲。 Scratch 是很好的培養學生的創新力、系統思維和協作的工具。正如 Scratch 的宗旨:
Scratch helps young people learn to think creatively, reason systematically, and work collaboratively — essential skills for life in the 21st century.
Scratch 不僅得到了 MIT 的支持, 哈佛大學也加入了 Scratch 的教育者培訓, 致力于培養更多的利用 Scratch 來教學的年輕老師和創新課程。

對于我們要面向的對象(8-12歲的少兒)來說,Scratch跳過了高級語言中那些繁難的概念和語法,用圖形化的表現和拖拽的交互來完成編程的核心邏輯和成果交付,既能解決學習曲線過于陡峭的問題,還能讓學習的過程不枯燥,并更及時地獲得結果反饋,非常適合他們這個年齡階段的心智水平和認知能力。
至于為什么要從Scratch開始作為階梯再緩慢過渡到高級語言,不如讓我們再來了解下8-12歲這個年齡段孩子的特點。
近代最具有影響力的瑞士兒童心理學家 讓·皮亞杰(1896-1980),把少年兒童的認知發展按照年齡劃分為了4個階段,而這同時,也構成了我們L0-L5課程設計所對應的理論依據:
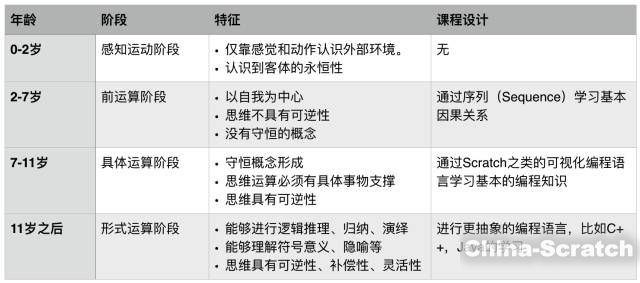
前運算階段的標志是符號功能的出現。這個階段的兒童的語言能力,以及玩耍時把棍子想象成槍的“假裝”能力,都是符號功能的體現。
但“前運算階段”的兒童對于守恒和可逆性這樣的邏輯運算的理解是有限的。
而在“具體運算階段”,兒童已經迅速獲得了認知操作能力,并能運用這些重要的新技能思考事物。具體運算思維表現為守恒的理解、關系推理的理解運算順序性的理解。但是,具體運算階段的兒童思維是有局限的,因為他們只能把運算圖式應用到真實的或可以想像得到的事物、情境或者事件上。
因此,在編程教育中,往往最早在“前運算階段”的后期,也就是6-7歲左右,并不會讓兒童直接接觸到邏輯和關系推理的概念。而是通過序列(Sequence)來讓兒童理解基本的因果關系。
同時,由于7-11歲“具體運算階段”的兒童的思維只能映射到具體的事物上,所以高級編程語言中的抽象邏輯、語言和教學方法是很難為這個階段的兒童所接受。Scratch就很好的解決了這個問題。在Scratch中,通過可視化的“積木”形式,兒童很容易把具象的結果和程序所對應起來,這樣就很好的避免了高級編程語言如C、C++等低反饋的學習流程。
所以針對7-11歲的兒童,Scratch的可視化語言可以很好的幫助學生學習基本的邏輯、關系推理、數學的概念,同時避免過早的接觸到“形式運算階段”之后才能理解的抽象的演繹推理。
聲明:本文章由網友投稿作為教育分享用途,如有侵權原作者可通過郵件及時和我們聯系刪除