資訊內容
用Scratch做一個3D引擎
同學們應該都接觸過3D游戲和3D動畫,那些栩栩如生的畫面,大家知不知道其實它們并不是照片,而是通過編程讓計算機實時畫(計算)出來的呢?今天我們就來學習3D動畫的基本原理,以及用scratch實現3D動畫的方法。

3D是英文3-Dimension,是三維的意思的。Dimension就是維度。3D就是指長、寬、高三個維度,或者說由x、y、z三個坐標軸構成的一種空間表示方法。它們構成了一個和我們現實生活一樣的立體空間。
在計算機科學家的努力下,現代計算機3D技術已經可以達到以假亂真的效果,基本上可以純粹通過計算來精確重現現實世界或者人們想象中的場景,其精確性、真實性和無限可操作性,使得3D技術可以廣泛應用于醫學、教育、軍事、娛樂等領域。
大家知道電視機、電腦顯示器、手機屏幕等實際上是2D(二維)的平面,它只有長和寬(只有x軸和y軸,沒有z軸)。要在2D平面上顯示出3D立體效果,就需要“3D引擎”,將立體物體的形狀、光線、運動等抽象成數學的表現形式,再通過計算輸出2D圖像,建立一個個真實的電腦世界。
Scratch沒有自帶的3D引擎。但是只要知道了3D動畫背后的原理,我們可以自己制作一個3D引擎出來。這就是我們一直強調的編程的好玩和強大之處:只要你學習、掌握了事物背后的原理,我們就有辦法通過編程把它模擬出來。
1.????坐標
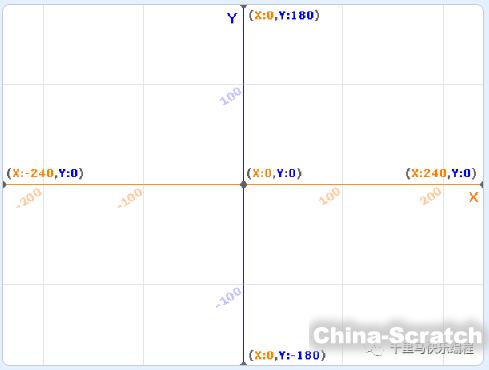
接觸過scratch的同學對于2D坐標已經非常熟悉:一個物體的x坐標代表它在屏幕左右方向的位置,y坐標代表它在上下方向的位置。Scratch規定了舞臺的坐標范圍分別是:x坐標范圍在-240到240,y坐標范圍在-180到180。?
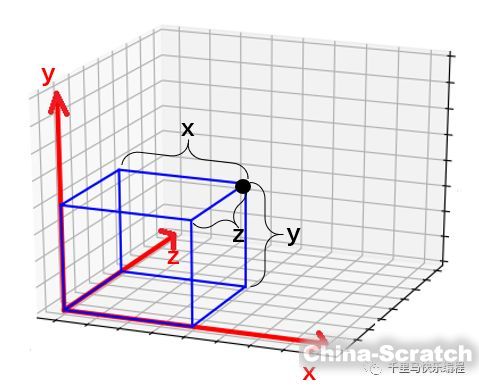
3D坐標系增加了一個z軸,其實就是2D坐標在縱深方向的擴展。如下圖所示,紅色直線代表x、y、z軸,黑色點的坐標(x,y,z)代表了它在三維立體空間中的位置。
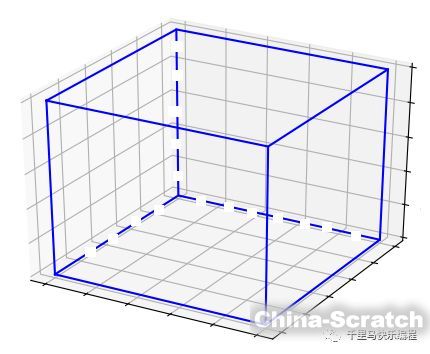
在scratch的2D舞臺上畫一個四邊形,我們需要知道四個頂點的坐標,然后把它們連線就可以畫出來。同樣道理,如果要在3D空間中畫出一個物體,一個方法是知道它的所有頂點的坐標,然后把頂點用直線連起來。比如下面這個立方體,把它的8個頂點連起來就能畫出來。
事實上,最復雜的3D圖案和最真實的3D動畫,背后都是通過這種方法畫出來。當然畫面細節越豐富,背后的數學模型越復雜,也需要越多的計算機資源(CPU、內存、顯卡)。作為入門介紹,本文只用最基本的3D圖形作為例子。
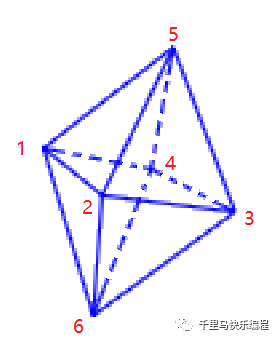
比如下面這個八面體,它有6個頂點,上半部分和下半部分分別有四個三角形。它是最簡單的可以一筆畫出來的多面體(上面的立方體就不能一筆畫出來,而八面體可以,同學們可以思考一下為什么),比如依次連接點1-6-2-5-3-6-4-5-1-2-3-4-1就可以不重復任一條邊把它畫出來。
簡單來說,只要我們知道了八面體的6個頂點的3D坐標,我們就能一筆過把它畫出來。
2.????投射
計算機屏幕是一個2D的平面,我們通過屏幕看到的3D物體,實際上是它根據透視原理在屏幕上的一個2D投射。
下圖說明了這個原理:視點代表了觀察者(眼睛或者攝像頭)的位置。藍色是一個3D物體,紅色平面代表了屏幕。綠色部分就是3D物體在屏幕上的投射。在屏幕上顯示一個3D物體,其實是顯示它在2D平面上的投射(綠色部分)。?
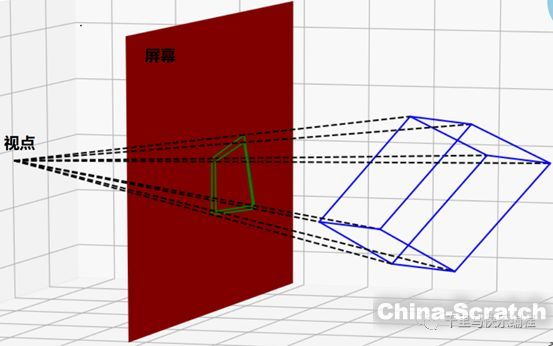
根據上圖可以知道,我們在屏幕上看到的一個3D物體的大小和形狀,其實跟以下幾個因素有關:
-
3D物體的實際位置
-
視點的位置
-
屏幕的位置
那3D空間某一個點投射在某個2D屏幕上的坐標是怎么計算的呢?請看下圖:
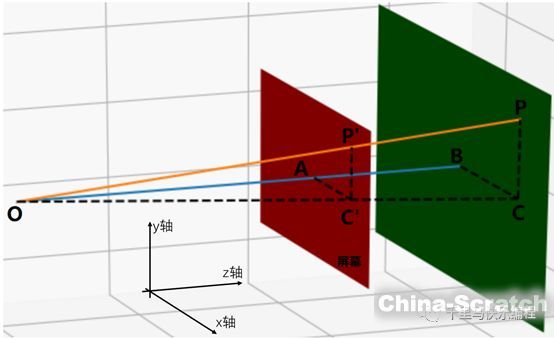
上圖中P代表3D空間中的一個點,設它的位置坐標值是x,y,z。現在要計算的是它在紅色的代表屏幕的平面上的投射點P’的坐標值。其中O點代表視點。
兩次強調,3D點的投射除了和它本身的坐標有關之外,還和視點位置、投射屏幕位置有關。這三個因素是互相影響的。忽略了任何一個因素都不能得出投射點坐標!
上圖中綠色平面代表P經過的、和紅色屏幕平面平行的一個平面。線段OAB和紅色以及綠色平面都垂直。為了方便計算,我們讓紅色平面與x軸和y軸組成的平面平行。這樣,線段OAB和z軸平行(并垂直于紅色及綠色平面);線段BC以及AC’與x軸平行;線段PC以及P’C’與y軸平行。
因為BC與AC’平行、PC與P’C’平行。根據相似三角形的特點,我們很容易知道:
OA /OB = AC’ / BC = P’C’ / PC
所以,如果知道:
-
P點坐標x,y,z
-
O點坐標ox,oy,oz
-
紅色平面的z坐標值pz
則:
OA = pz – oz
OB = z – oz
BC = x – ox
PC = y - oy
則P在紅色屏幕平面投射點P’的x、y軸坐標值為:
-
P’的x坐標 =
ox + AC’ =
ox + [(pz – oz) * (x - ox)/(z - oz)] -
P’的y坐標 =
oy + P’C’ =
oy + [(pz - oz) * (y - oy)/(z - oz)]
接下來我們就用這個結論在scratch里畫出一個3D的八面體來。
Scratch的2D舞臺就是上面圖中的紅色屏幕,我們要做的就是把3D物體在2D屏幕上的投射畫出來。所以在畫(編程)之前我們先要在自己心中有一個3D坐標,視點的位置、屏幕的位置、物體的位置我們都要先想清楚。
八面體有6個頂點,如下圖依次連接點1-6-2-5-3-6-4-5-1-2-3-4-1就可以一筆過畫出它來:

-????? 首先我們用三個數組分別保存八面體6個頂點的x坐標、y坐標和z坐標:
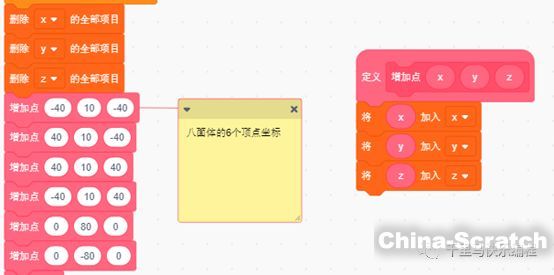
-????? 定義視點及投射屏幕平面的位置(前面說過,為了方便計算,我們讓投射平面與x軸和y軸組成的平面平行,所以投射面只有一個z值)

-????? 根據前面3D到2D屏幕的投射公式,自定義一個積木用來投射轉換:
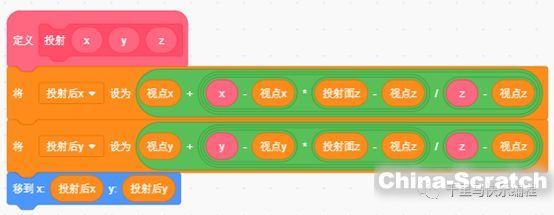
-????? 接下來就依次投射1-6-2-5-3-6-4-5-1-2-3-4-1點,用畫筆畫出連接各點的軌跡。
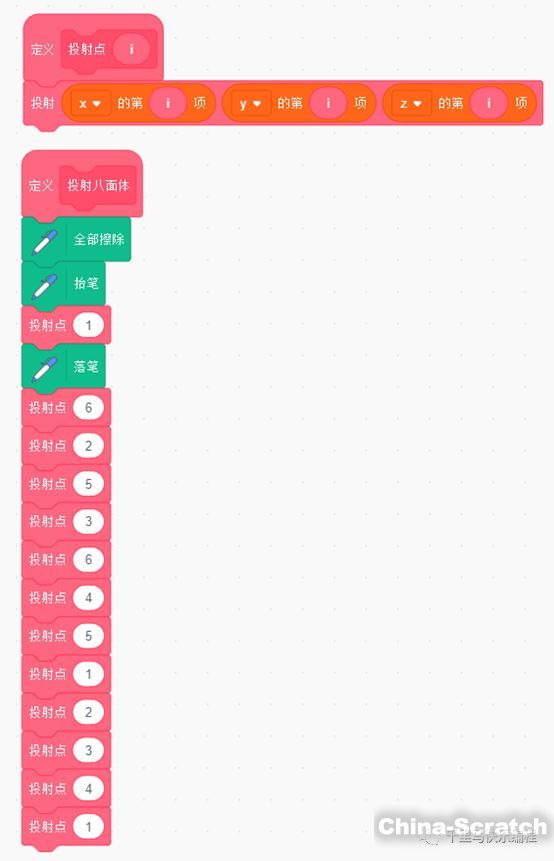
執行“投射八面體“積木就可以畫出下面的形狀:
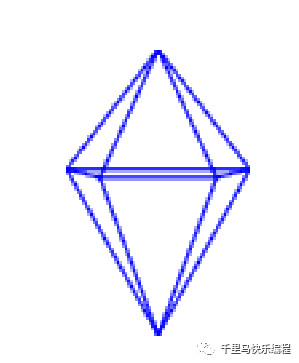
3.????移動
?
物體移動只需要改變它所有頂點的x,y,z值,然后再重新投射一次就可以了。實現程序如下:
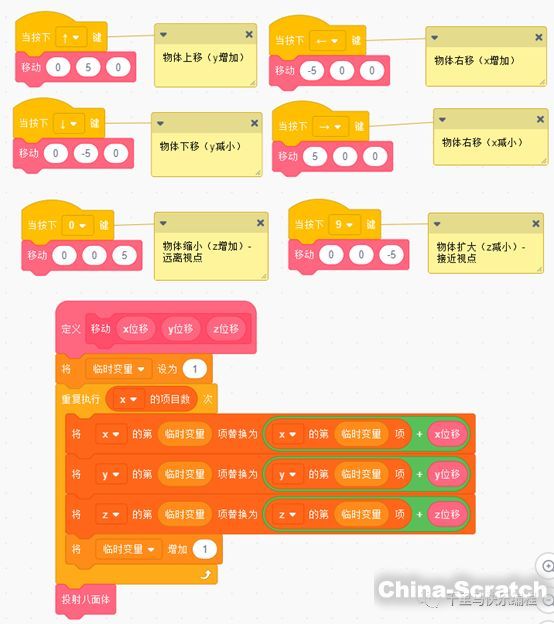
注意這里物體的移動是在原3D空間的移動,所以物體在x軸方向或y軸方向移動后,在屏幕上的投射會產生一定的旋轉效果。視點離投射平面越近,這種旋轉效果越明顯。
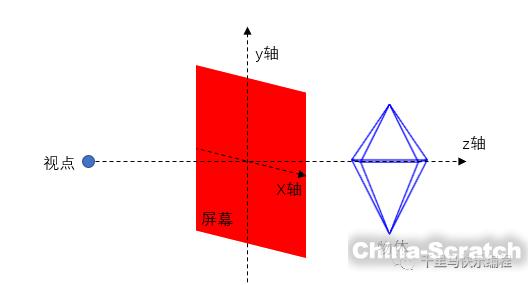
物體在z軸方向的移動會產生物體大小變化的視覺效果:物體遠離視點時物體投射縮小,接近視點時物體投射增大。原理如下圖所示:
?
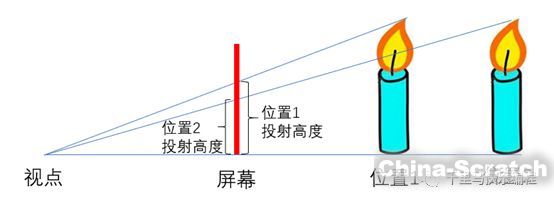
移動的效果如下:

4.????旋轉
物體旋轉涉及到三角函數的知識。推導過程需要一定的篇幅。我們只需要記住簡單的結論來應用就可以了。
旋轉可以分為三種:沿x軸的旋轉、沿y軸的旋轉和沿z軸的旋轉。
-????? 沿x軸旋轉時,物體的x坐標不變,y坐標和z坐標的變換規律是(A為旋轉角度):
新的y坐標 = y * cos A + z * sin A
新的z坐標 = z * cos A - y * sin A
-????? 沿y軸旋轉時,物體的y坐標不變,x坐標和z坐標的變換規律是(A為旋轉角度):
新的x坐標 = x * cos A - z * sin A
新的z坐標 = x * sin A + z * sin A
-????? 沿z軸旋轉時,物體的z坐標不變,x坐標和y坐標的變換規律是(A為旋轉角度):
新的x坐標 = x * cos A - y * sin A
新的y坐標 = x * sin A + y * cos A
下圖顯示了沿z軸旋轉時的變換情況。有興趣的同學可以自己推導出坐標的變換規律。
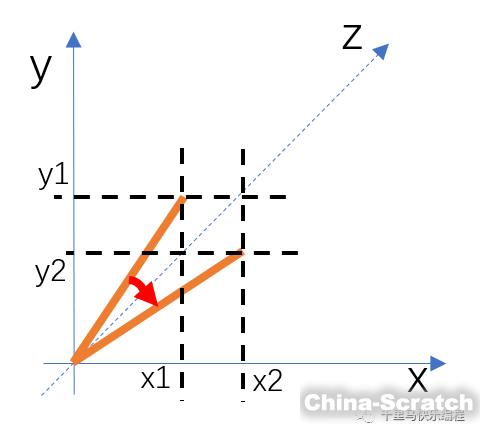
注意上面說的坐標變化都是物體原3D坐標的變化,而不是投射在2D平面上的投射坐標的變化。換言之,旋轉改變物體坐標后,還要重新計算投射坐標。
旋轉的實現方法:
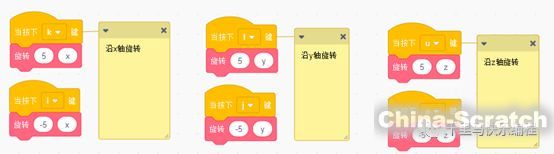
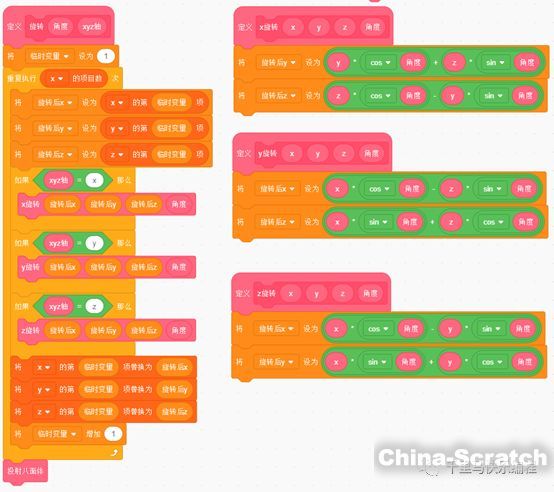
效果如下:

本文原程序可以在這個鏈接找到:
https://scratch.mit.edu/projects/282534568/
再給大家分享一個3D煙花動畫,主要也是運用了本文介紹的方法制作的3D效果。具體的制作方法有時間再給大家分享。
https://scratch.mit.edu/projects/282581016/
5.????結語
今天我們學習了基本的3D引擎制作方法。當然這是最最基本的3D知識,大家看到,即使是最基本的3D原理,已經用到不少的幾何和三角函數知識。對有志于研究最新3D技術的同學,比如3D游戲、VR(Virtual Reality虛擬現實)、AR(Augmented Reality增強現實)、3D打印等等,請進一步打好數學和編程基礎。
事實上3D等圖形顯示技術屬于一門叫做計算機圖形學的學科。計算機圖形學可以幫助人腦從圖形圖像的角度理解事物本質。在科學、娛樂、藝術、設計等領域,計算機圖形學都起著重要的基礎作用。期待有志于此的千里馬學員以后能創造出一個又一個的視覺奇跡。

聲明:本文章由網友投稿作為教育分享用途,如有侵權原作者可通過郵件及時和我們聯系刪除



