您現在的位置是:首頁 » scratch編程資訊
資訊內容
scratch算法練習-矩形填充
極客小將2023-08-16-
scratch算法練習-矩形填充題目出自CCF計算機程序設計入門篇練習(基本要求能夠理解除法,思路很重要)題目描述已知矩形的大小為nm,現用aa的正方形填充該矩形。輸入三個正整數n,m,a(n,m,a≤10^3),計算至多能填入多少正方形?(正方形可以正好碰到矩形邊界,但不能超出矩形
scratch算法練習-矩形填充
題目出自CCF計算機程序設計入門篇練習(基本要求能夠理解除法,思路很重要)
題目描述
已知矩形的大小為n×m,現用a×a的正方形填充該矩形。輸入三個正整數n,m,a(n,m,a≤10^3),計算至多能填入多少正方形?(正方形可以正好碰到矩形邊界,但不能超出矩形外)
輸入
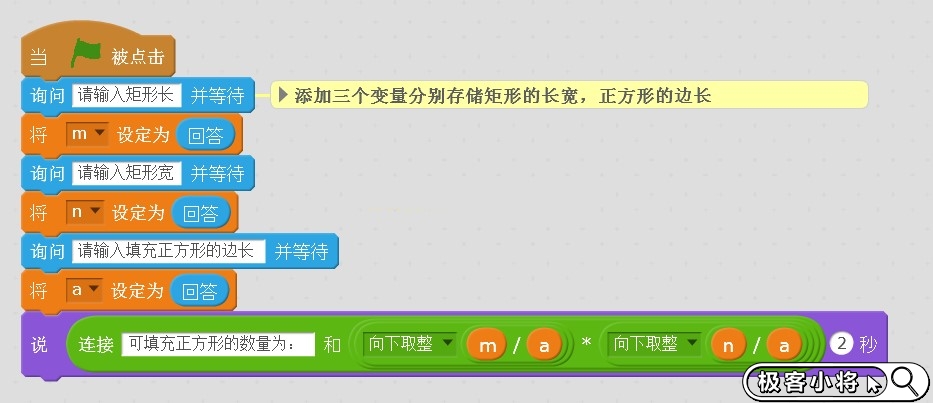
通過詢問輸入三個正整數n,m,a,例如:3 4 1
顯示
能填入正方形的數量。如:12
思路:
(1)將理解題目,將問題轉化為數學模型
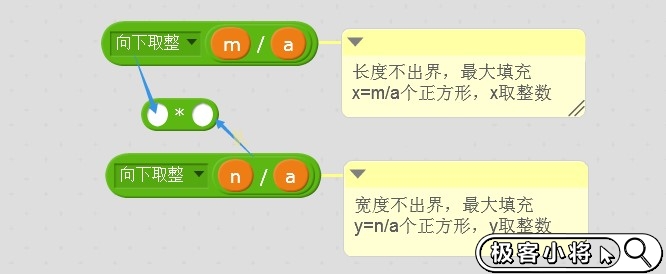
(2)長度不出界,最大填充x=m/a個正方形,x取整數。
(3)寬度不出界,最大填充y=n/a個正方形,y取整數。
(4)n*m的矩形最多填充x*y個邊長為a的正方形。
(5)填充的矩形為正方形(特殊情況),沒有方向性,也符合上述方法

- 上一篇

scratch算法練習階乘求和
scratch算法練習階乘求和階乘是基斯頓卡曼(Christian Kramp,1760~1826)于 1808 年發明的運算符號,是數學術語。一個正整數的階乘(factorial)是所有小于及等于該數的正整數的積,并且0的階乘為1。自然數n的階乘寫作n!。1808年,基斯頓卡曼引進這個表示法。亦即n!=123...
- 下一篇
scratch算法練習-列表插入并排序
scratch算法練習-列表插入并排序題目:有一個已經排好序的列表。scratch生成一個隨機數,要求按原來的從小到大順序將它插入數組中。程序分析:首先判斷此數是否大于等于最后一個數,是的話就添加到列表里(因為向列表末尾添加數是不能通過插入來實現的),否則考慮插入中間的

