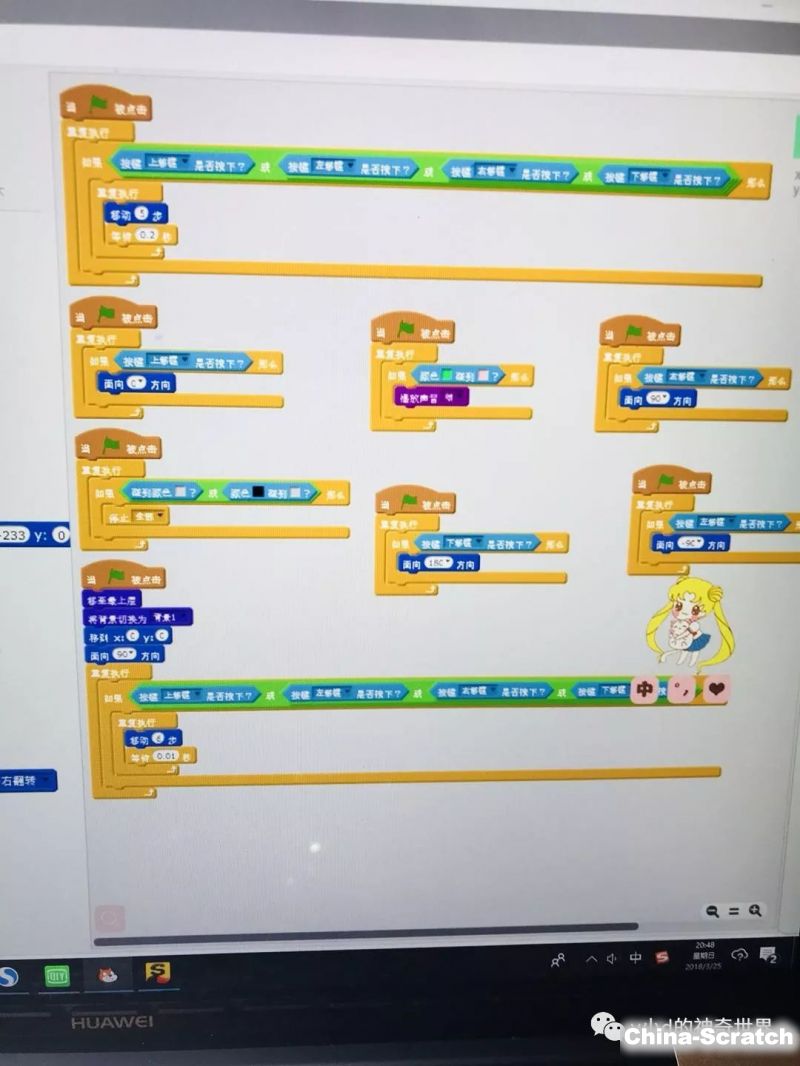
資訊內容
使用Scratch證明:周長一定時正多邊形面積最大
吳俊杰老師于17年7月初發布了一道Scratch題目,如圖所示。經過4個小時的奮戰,我終于搞定了這道題目。下面我對本程序進行匯整、說明:首先介紹數學反證法證明周長一定時正多邊形面積最大;接著介紹Scratch反證法的思路;然后介紹程序的操作方法;最后介紹程序的數學原理以及設計思路。
一、數學證明
首先證明等周定理,然后利用等周定理即可得到推論:等周多邊形面積最大是其正多邊形。等周定理的定義:在周長一定的所有封閉平面曲線中,圓所圍的面積最大。下面先來證明等周定理。證明:設K是周長一定而面積最大的圖形,只要證明K是一個圓即可。以下分三步來完成。
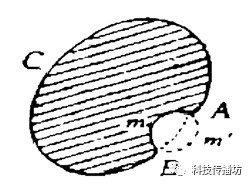
第一步:用反證法證明K是凸多邊形。如下圖所示,若K是一個凹圖形, 那就一定可以在它上面找到兩點A、B,其連線落在圖形K的外部。以AB為軸,把曲線AmB對稱到另一側,稱為曲線Am’M。圖形AmBC與圖形A m’BC的周長相等,而后者面積更大,這與K有最大面積矛盾。故K只能是凸圖形。
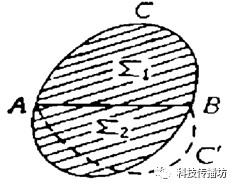
第二步:用反證法證明平分K的周長的弦也一定平分其面積。如下圖所示,設凸圖形K有最大面積,AB平分它的周長,且弦AB把K分成兩部分Σ1和Σ2。Σ1≠Σ2,不妨設Σ1>Σ2,以AB為軸,把ACB對稱到另一側AC’B處,則周長ACBC’A等于K的周長,但面積ACBC’A>K的面積,這與K有最大面積矛盾。所以,平分K的周長的弦也一定平分其面積。
第三步:證明平分周長、面積的弦是直徑,從而K為圓。?用反證法。設AB平分K的周長和面積,在K的邊界上任取一點C,只需證ACB為半圓。若不然,∠ACB≠90°,將下圖左側中的Σ1、Σ2剪下來,貼成另一個圖形(下圖右側),其中A’C’=AC,B’C’=BC,∠A’C’B’=?90°。這兩個圖形中,曲線ACB的長等于曲線A’C’B’的長,但后者面積較大,與K有最大面積矛盾。故ACB為半圓,從而K是圓。
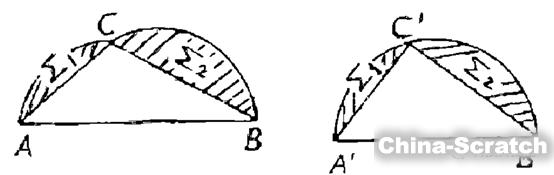
于是,證得了等周定理:在所有等周的平面封閉圖形中,以圓的面積為最大。下面證明周長相等的多邊形中,正多邊形的面積最大。
證明:在所有周長相等的圖形中,正多邊形與圓形最接近,由等周定理的定義可知,正多邊形的面積最大。
參考文獻
《探索等周定理的推廣及其應用》
https://wenku.baidu.com/view/277a9c6169eae009581bec99.html
二、Scratch反證法
根據之前的證明可知正多邊形面積最大,因此本程序可能的設計思想如下:
-
展示如上數學證明思路。這樣做雖然簡單,但是很抽象,需要用戶詳細地跟隨程序的指引完成證明過程。
-
給定正多邊形,讓用戶拖拽多邊形頂點,同時保證等周的條件。如果用戶找不到更大面積的情形,即反證了本題目。這樣做雖然復雜,但是用戶體驗好,且有數學證明保證正確性。本程序選擇此設計方法。
三、程序操作說明
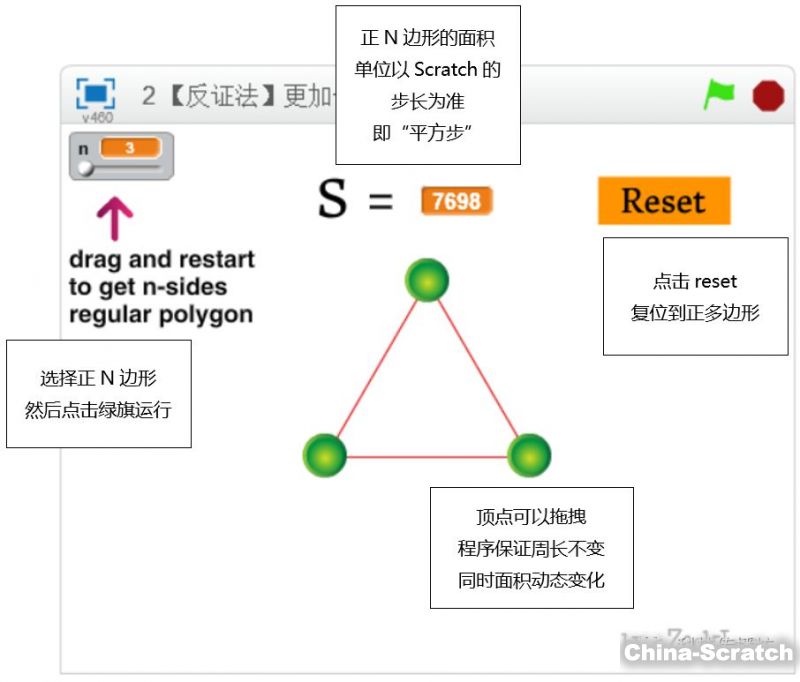
四、程序數學原理
?????? 本程序的難點在于拖拽頂點時保證等周,即周長不變。顯然,橢圓的第一定義可以滿足這一點:平面內與兩定點F1、F2的距離的和等于常數2a (2a>|F1F2|) 的動點P的軌跡叫做橢圓。即 |PF1|+|PF2|=2a。
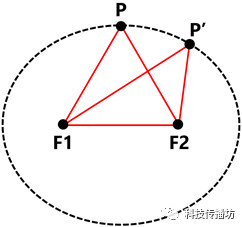
根據定義可知,F1P+F2P=F1P’+F2P’,這就是等周的關鍵。當點擊某個頂點時,得到左右相鄰兩頂點的坐標,以此作為橢圓的兩焦點,計算F1P+F2P后即可得到橢圓的各個參數,然后限制頂點P的移動再次橢圓軌跡上即可保證等周。橢圓的一般化參數方程如下:
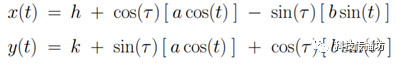
其中參數t決定了頂點位于橢圓線上的位置,可以設置為鼠標在舞臺上的角度;參數τ是橢圓和x軸的夾角;參數a、b是橢圓的長短軸長度;(h, k) 是橢圓中心點所在坐標。
參考文獻
《Using the Ellipse to Fit and Enclose Data Points》
http://www.cs.cornell.edu/cv/OtherPdf/Ellipse.pdf
五、程序細節展示
?????? 本文僅展示核心腳本。當點擊某個頂點后,程序會尋找該點左右相鄰的兩個頂點坐標:
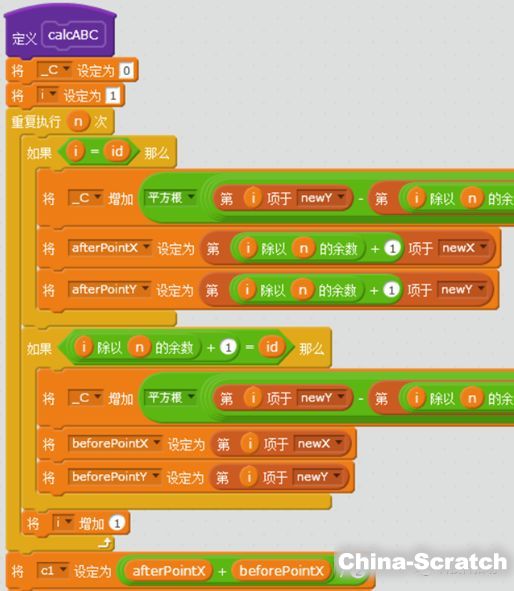
變量beforePointX和beforePointY是第一個相鄰點(即橢圓的第一個焦點)的XY坐標,變量afterPointX和afterPointY是另一個相鄰點(即橢圓的第二個焦點)的XY坐標。變量_C保存了當前頂點到兩焦點的長度和,即橢圓第一定義中的2a。接著計算橢圓參數方程中的關鍵參數:
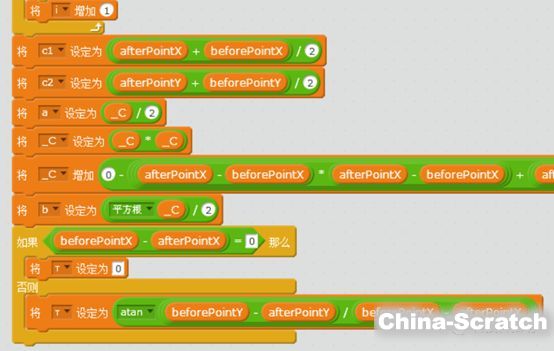
變量c1c2顯然是橢圓中心點位置,即參數方程中的 (h, k);_C除以2即橢圓的半長軸a;根據橢圓a2-b2=c2可以計算變量b的值;最后計算τ,需要注意水平情況,即在橢圓未發生傾斜時,斜率公式分母為0,所以要特殊處理。得到基礎數據后便可設置頂點的位置:

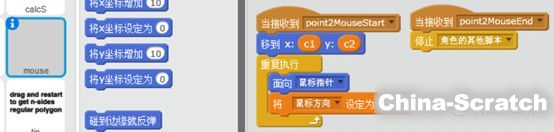
變量鼠標方向就是參數方程中的t,設置為鼠標的當前方向:
聲明:本文章由網友投稿作為教育分享用途,如有侵權原作者可通過郵件及時和我們聯系刪除