親愛(ài)的朋友們，相信你們都用畫(huà)筆來(lái)畫(huà)過(guò)三角形、正方形、五邊形等圖形對(duì)吧。你們想不想知道還可以用更酷的方式來(lái)畫(huà)這些多邊形呢？CODER這次就帶你用scratch編程方式來(lái)實(shí)現(xiàn)這些效果哦。

01

效果圖

我們先來(lái)看看，正三邊形、正四邊形、正五邊形、正六邊形等等，通過(guò)旋轉(zhuǎn)形成的美麗的分形圖形吧！

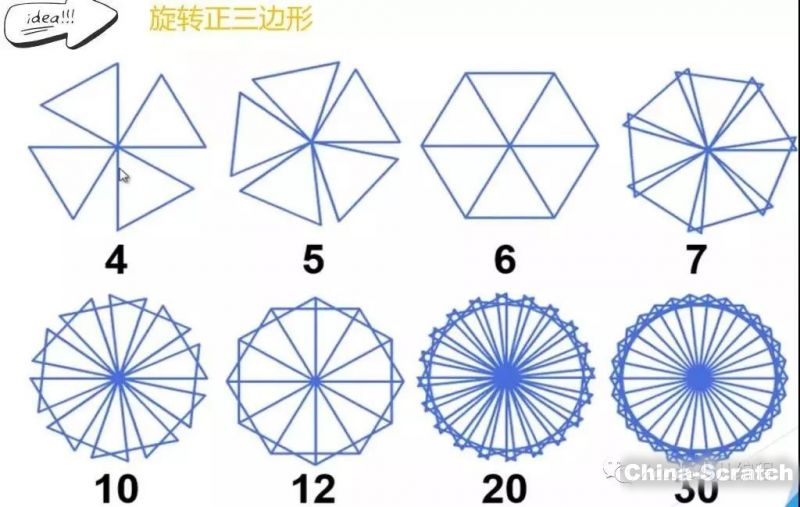
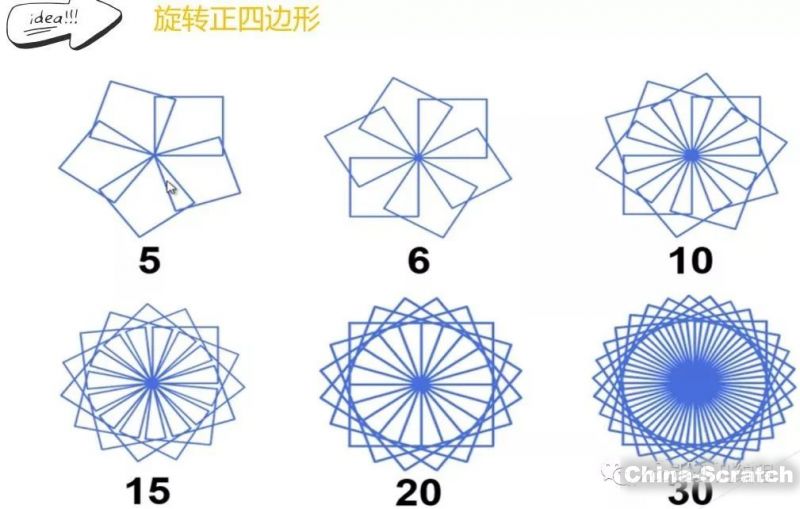
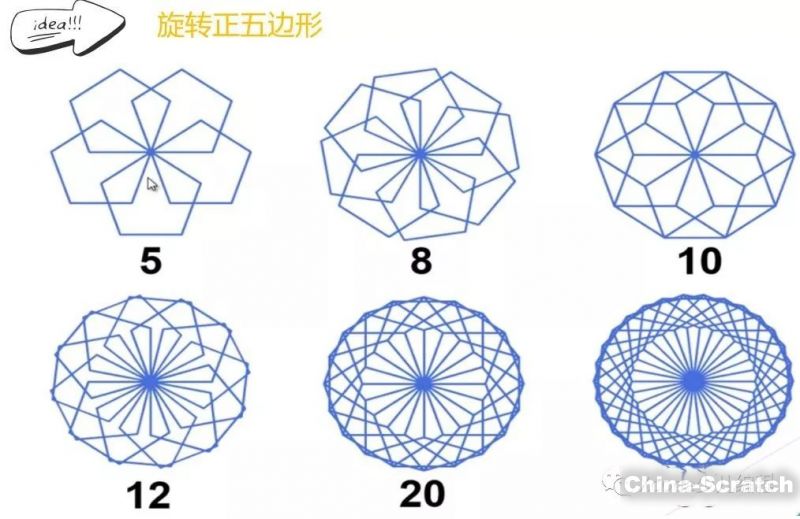
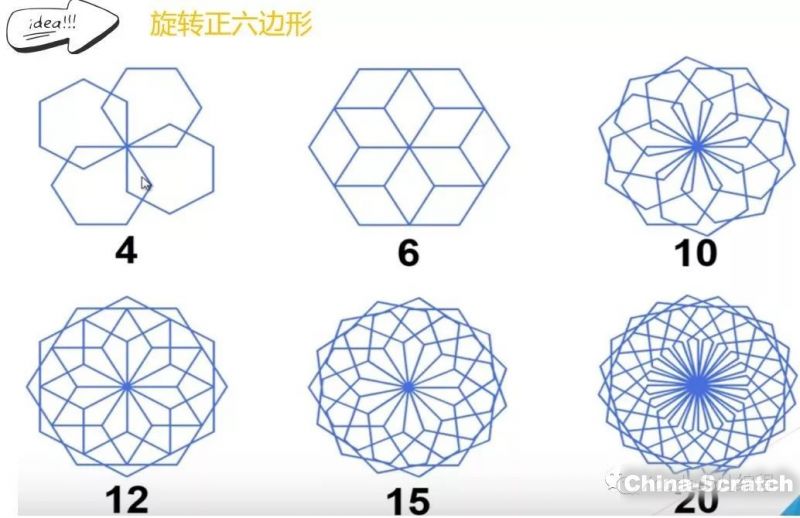
效果圖

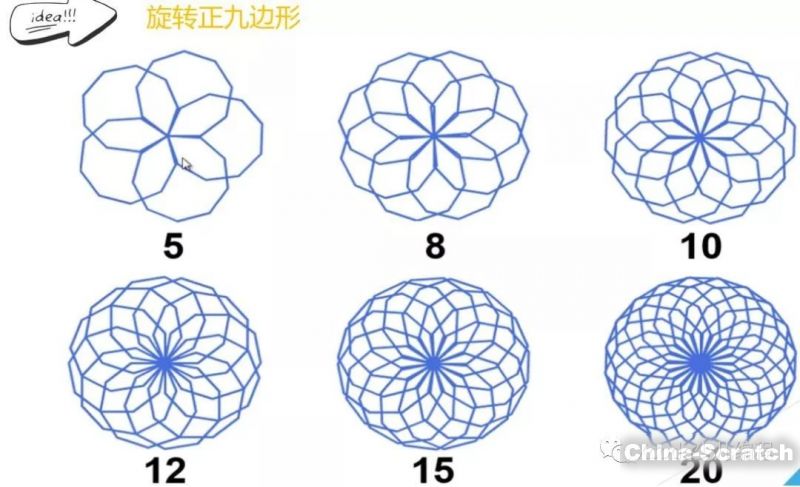
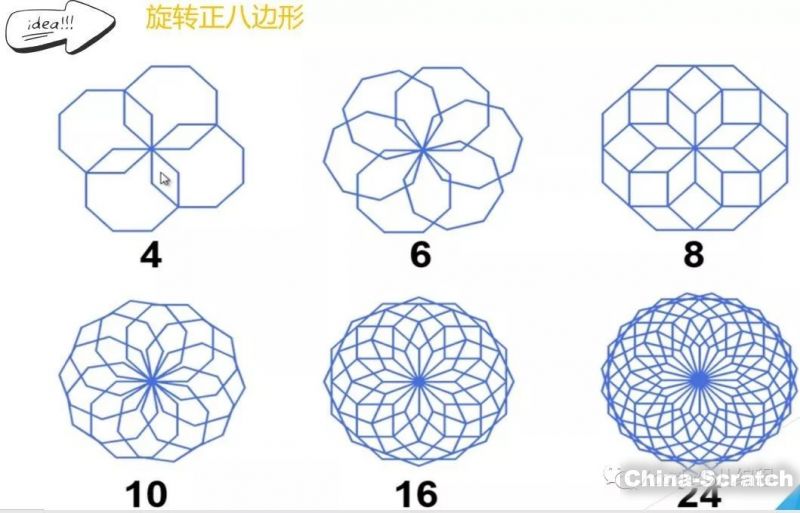
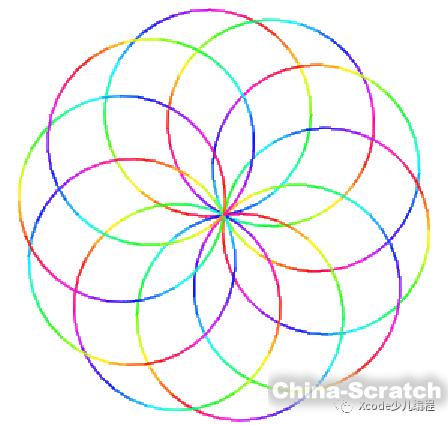
*此處可以向右滑動(dòng)*

02

編程思路

繪制圖形要用到運(yùn)動(dòng)積木的旋轉(zhuǎn)角度和畫(huà)筆積木。因?yàn)橐?huà)正多邊形旋轉(zhuǎn)的分形圖形，所以同樣用到控制積木的重復(fù)執(zhí)行。繪制正多邊形需要用到數(shù)學(xué)知識(shí)任意多邊形的外角和等于360°。

第一：先來(lái)看看運(yùn)動(dòng)積木的旋轉(zhuǎn)角度（如圖1）向右是面向90°，向左是面向-90°，向上是面向0°，向下是面向180°。

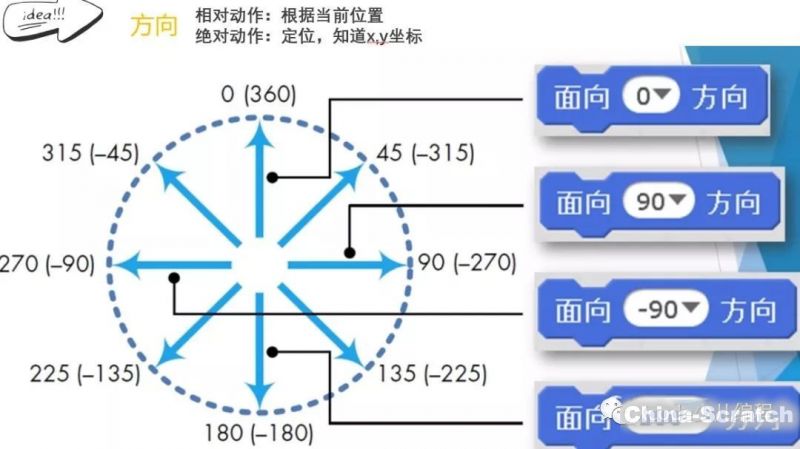
圖1

第二：繪制正多邊形的旋轉(zhuǎn)角度思路(如圖2）

畫(huà)旋轉(zhuǎn)的圖形，旋轉(zhuǎn)的都是外角。我們都知道任意多邊形的外角和等于360°。所以在繪制正多邊形時(shí)，旋轉(zhuǎn)的角度等于360°除以正多邊形的邊數(shù)。

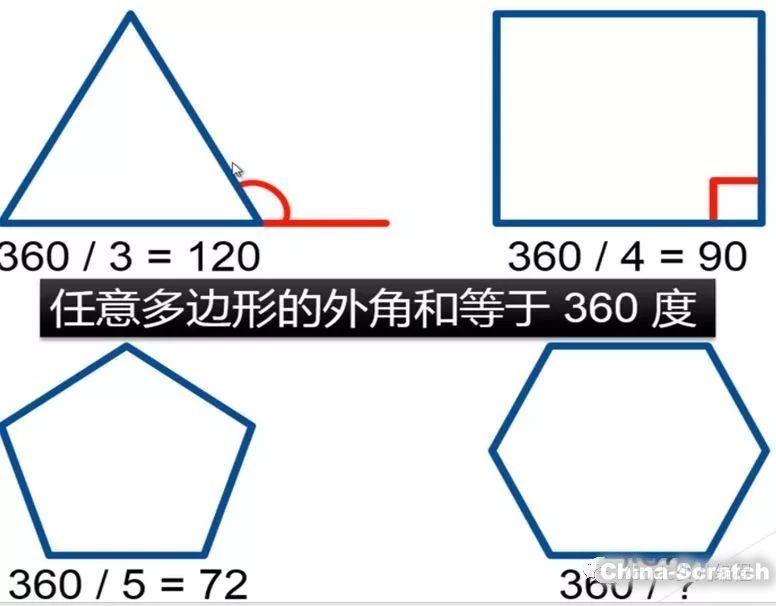
圖2

03

腳本展示

正四邊形

讓我們一起來(lái)看看繪制正四邊形的腳本展示吧(如圖3)

腳本分析：

第一步:當(dāng)綠旗被點(diǎn)擊時(shí)，初始化方向向右，移到原點(diǎn)。

第二步：初始化筆的顏色，可以設(shè)置你喜歡的顏色哦。畫(huà)筆顏色的值：0代表紅色 70代表綠色? 130代表藍(lán)色? 170代表粉色 。然后初始化畫(huà)筆的粗細(xì)，進(jìn)行繪制之前，要先擦除，然后落筆。

第三步：因?yàn)槭抢L制正四邊形，所以正四邊形的每條邊的大小都相等，就是一個(gè)重復(fù)執(zhí)行的循環(huán)。另外旋轉(zhuǎn)的角度為360°/4=90°

最后完成啦！小朋友動(dòng)手實(shí)現(xiàn)一下吧

可以嘗試?yán)L制一下以下圖形哦

三邊形：3次 120度

四邊形：4次 90度

五邊形：5次 72度

六邊形 ：6次 60度

......

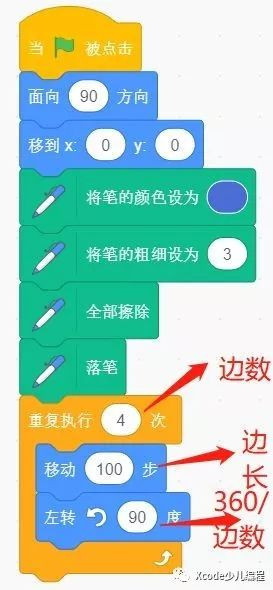
圖3

圓

接下來(lái)我們一起來(lái)看看如何畫(huà)圓吧

圖3

分形圖形思路

下面看看分形圖形的思路吧（如圖4）

繪制分形圖形就是一個(gè)正多邊形旋轉(zhuǎn)而成。例如繪制正四邊形的分形圖形，就是在繪制完正四邊形后，然后添加一個(gè)外層循環(huán)，循環(huán)次數(shù)可以是浮點(diǎn)數(shù)類(lèi)型，不一定要整數(shù)類(lèi)型。只要旋轉(zhuǎn)次數(shù)*旋轉(zhuǎn)角度=360°即可。

可以嘗試以下的組合：

（1）5次 72°????? （2）10次? 36°

（3）72次 5°??????? （4）36次 10°

注意：若速度慢，使用加速度模式

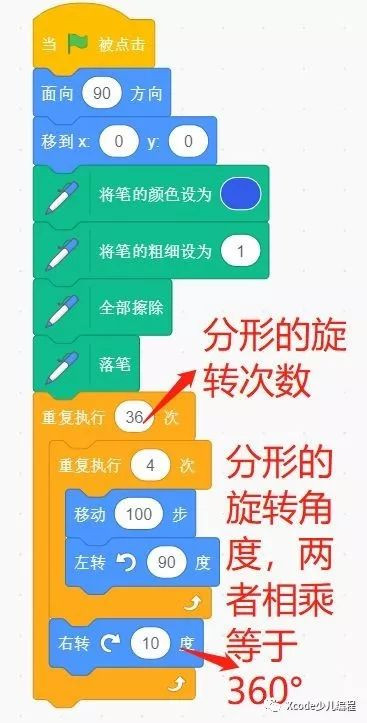
圖4

當(dāng)然，也可以通過(guò)自己手動(dòng)繪制其他圖形，然后通過(guò)旋轉(zhuǎn)和圖章，形成其他的圖形！例如（圖5）

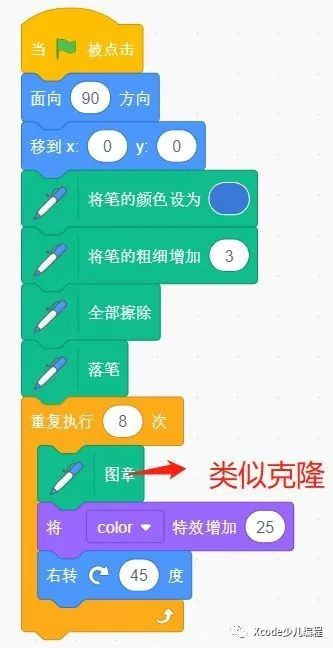
圖5

其他特別的三角形

想要做其他的三角形，需要我們先來(lái)認(rèn)識(shí)一下正弦定理和余弦定理（如圖6）

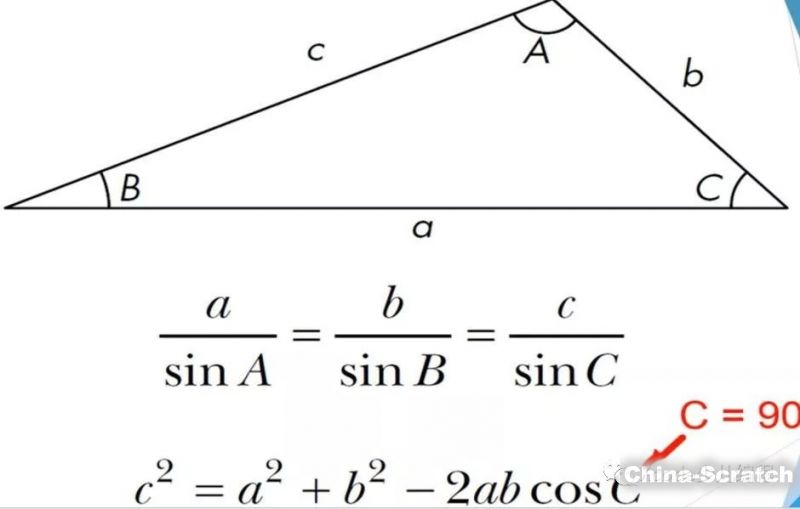
圖6

等腰直角三角形

我們一起來(lái)看看等腰直角三角形的思路（如圖7和圖8）

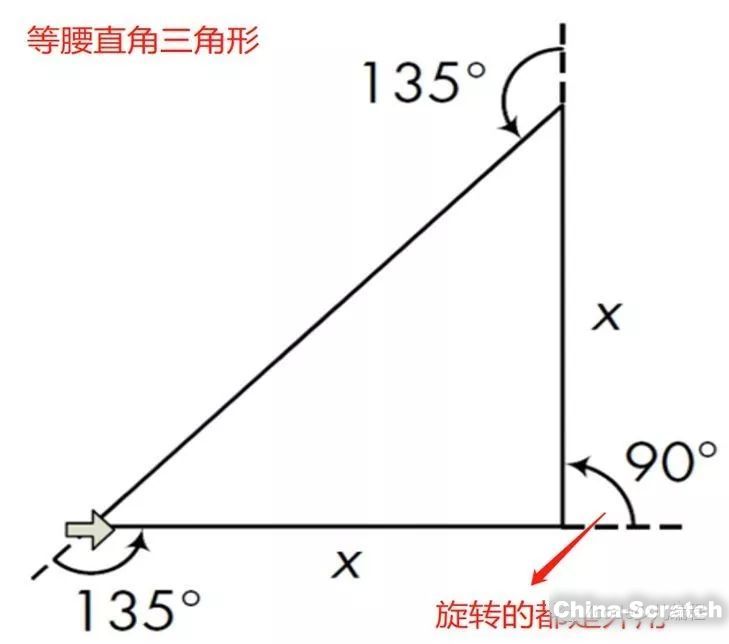
圖7

圖8

繪制等腰直角三角形方法總結(jié)：移動(dòng)x步，左轉(zhuǎn)90°，然后再移動(dòng)x步，左轉(zhuǎn)135°。移動(dòng)2x步，再旋轉(zhuǎn)135°（如圖9）

圖9

30°-60°-90°三角形

現(xiàn)在來(lái)聊聊30°-60°-90°三角形吧（圖10、圖11）

圖10

圖11

3：4：5三角形

繪制3：4：5三角形，有一個(gè)規(guī)律是邊長(zhǎng)是3x,4x,5x，然后求出每個(gè)角度，即可繪制出來(lái)。（如圖12、圖13）

圖12

圖13

還可以繪制任意三角形呢

圖14

繪制矩形

圖15

繪制平行四邊形

圖16

圖17

繪制梯形

圖18

繪制風(fēng)箏形

圖19

PS:scratch雖然是一個(gè)鼠標(biāo)拖拽為主的，模塊型編程，但與其他編程形式相同的是：提出問(wèn)題——分析問(wèn)題——解決問(wèn)題，其中最主要的是將大問(wèn)題分解成一個(gè)個(gè)小問(wèn)題，然后利用自己已經(jīng)學(xué)過(guò)的知識(shí)進(jìn)行有針對(duì)性的解決，這就是編程思維，也是我們?nèi)粘Ｉ顚W(xué)習(xí)工作中需要善加利用的邏輯思維。

聲明：本文章由網(wǎng)友投稿作為教育分享用途，如有侵權(quán)原作者可通過(guò)郵件及時(shí)和我們聯(lián)系刪除